Aldo Piana     

Part  IV

The gravitational Waves in quantum space. Their origin, characteristics and performances.

PART IV : CONTENTS

    21) THE GRAVITATIONAL WAVES

(To PART I)    

(To PART II)    

(To PART III)    

(To HOME PAGE)    

(To INDEX)    

In spite of the many attempts made, in spite of researchers’ efforts and the use of complex, highly sensitive equipment, gravitational waves, predicted by relativity,  still have not been revealed, except for few rather unreliable indications.

However, are we certain that they are searched for in the right places and in the right ways, and that everybody means the same thing by gravitational waves?

In order to understand the reasons causing difficulties in this kind of search, to explore any alternative investigation available and to make sure that no misunderstanding exists about the subject of this research, I believe it will be useful to completely re-examine this topic, starting from the ways gravitational waves form, up to the action they perform. This analysis is obviously made in the framework of quantum space theories, but many considerations can also apply to other contexts, with an appropriate translation.

In quantum space, mass is hypothesized as a halo surrounding material particles. The halo, made up of a shell of small-sized space quanta “contaminated” by the particle’s energy, will interact with space, thus determining its curvature. In other words, mass behaves like a gas bubble in a liquid; the bubble displaces the liquid’s molecules, causing them to arrange themselves spherically around it.

For complex objects, the curvature imprinted on space is equal to the sum of the curvatures determined by all constituent particles, but in this case it is not a perfect sphere, but rather an overlapping of spheres, each centered on a constituent.

Thus space will acquire an unlimited  pseudo-spherical  configuration, centered on the particle or on the object, a sort of “gravitational bubble” which interacts with the curvature imprinted on space by nearby bodies, determining as a whole the spatial geometry in which objects move.

Obviously the influence each object exerts on geometry as a whole is proportional to its mass.

The objects however are in motion along the track determined by space geometry itself. The track they follow, seen from the object as a straight line, from the outside looks like a circular or elliptical orbit, or less frequently like another curve of the family of conic sections, which follows the curvature of space determined by the body around which the object revolves. From a greater distance, when the observation field includes a higher number of objects, the track will first look like a cycloid, then like an overlapping of cycloids of increasingly large size.

The orbits’ tracks however are not as regular as they may seem at a first observation, because they exhibit imperceptible irregularities not only caused by the irregularities of curvature itself, as pointed out before, but also by the fluctuation of the geometrical configuration; more precisely, they shall be considered as statistical successions of all the positions the moving body can take in a given time frame. The smaller the object, the larger orbital irregularities determined by the geometrical configuration will be.

The object’s motion along its orbit corresponds to the orbital shift of the relative “gravitational bubble” which in turn produces a gravitational perturbation on surrounding objects in the form of waves. The wave’s frequency corresponds to the orbital period: it is extremely high for elementary particles, (in quantum space with a stepwise digital track, rather than continuous analogical profile) and it rapidly decreases as the bodies’ size and complexity increase.

Moreover the gravitational wave produced by a complex object exhibits a profile which retains the trace of the waves generated by the mutual motions of all its constituents; the total wave is the sum of all concurrent waves.

A peculiar characteristic of the gravitational wave produced by bodies in orbital motion is its spatial distribution. The wave does not propagate spherically; it exerts the strongest perturbations in a sinusoidal way on the bodies lying on the rotation plain of the object that generates it. The bodies lying near the rotation axis instead will only be subjected to a disturbance which tends to cause their rotation axis to oscillate with a precession pattern. 

Intermediate positions are characterized by a combination of sinusoidal and precession perturbations, according  to the perturbed object’s angular position on the rotation plain of the body generating the wave. Setting aside the detection difficulties for a moment, the wave’s degree of polarization could provide precise indications regarding the orientation of the body that generated it.

Bodies in orbital motion however are not the only source of gravitational waves: any mass variation in a given region of space is at the origin of gravitational perturbations on external bodies. It follows that explosion, expansion, collapse and mass-energy conversion events, as in supernova explosions, will lead to the most intense gravitational perturbations; their undulatory pattern is however highly irregular, whereas violent mass-energy conversion will generate negative, brief impulses  restricted to the time taken by conversion.

In such cases the spatial distribution of gravitational impulses will be spherical in the event of mass-energy conversions and homogeneous explosive expansions, and irregular in the event of expansion made inhomogeneous by varying waves of densities.

Gravitational waves produced by supernova explosions are the most intense, but also the hardest to detect because of their duration and irregularity patterns, and because of the overlapping of waves with extremely diverse frequencies  and phases at negative impulses. Moreover, the presence of a background of waves coming from every object in the universe which permeates space makes their identification even more difficult.

Sufficiently intense and regular gravitational waves can be generated by double-star or multiple-star systems, which are present in high percentages (estimated at almost 50%) both in the Milky Way and in other galaxies. Pairs of stars which differ greatly in mass, type, and age   are not suitable for the study of the gravitational waves they produce, as they exhibit complex interaction phenomena which strongly alter their behavior. Pairs of stars with equal mass and characteristics instead constitute the ideal object of study.

One of the systems that has been studied for a long time is the pair of coalescent neutron stars  PSR 1913+16, one of which is a pulsar, discovered by Taylor and Hulse in 1974 and observed for nearly two decades with the arecibo radio telescope.

The PSR 1913+16 pair is composed of two neutron stars - each with a mass of 1.4 M$ (solar masses)  approaching the black hole limit, with an estimated diameter slightly over 10 km – which revolve around their common center of mass with highly elliptical orbits at a mutual distance of about 770,000 km at periastron and about 3,340,000 km at apastron. The orbital period is about 7 hours and 45 minutes long.

The prolonged observation has allowed the determination of the pulsar’s revolution around the periastron, similarly to the advancement of Mercury’s perihelion, perfectly in line with relativity’s predictions. The advancement of the pulsar’s periastron is 4.2 degrees per year: in only one day it equals Mercury’s perihelion’s shift in one century.

But the system’s most relevant feature is the orbital period’s decrease of 76 milliseconds/year, which presumably indicates a loss of energy attributable to the emission of gravitational waves. The decrease of the orbital period and the consequent contraction of the orbit will cause the two stars to merge in about 300 million years.

The  PSR 13+16 pair therefore seems to be a possible source of intense and regular gravitational waves which should be relatively easy to pick up with the new detectors under construction (Virgo in Medicina, Ligo at Hanfor and Livingston, and others currently designed or under construction in Japan and the space interferometer LISA with a base of 5 million km scheduled for 2010), especially if used in combination.

It must however be pointed out that the more elusive waves that these instruments will try to detect are not exactly the gravitational waves which originate in the ways discussed above, but rather an effect they cause.

We must then distinguish between the gravitational perturbation exerted on surrounding objects by accelerating masses (or orbiting masses, which is the same thing) and space-time contracting or expanding oscillations stemming from the perturbations, i.e. the “waves” predicted by relativity.

A recent work carried out at the Department of  Physics and Astronomy SUNY, Stony Brook, NY, emphasizes this distinction and suggests that it may be incorrect to use the term gravitational waves to define structural oscillations of the space-time. Below is their complete statement:

To avoid any misunderstanding we may then speak of “gravitational waves” and “relativistic gravitational waves” still making sure that their characteristics, formation modes, and effects remain clearly distinct until they overlap.

We don’t need to go too far to find gravitational waves intended as perturbations of the gravitational field caused by nearby masses in motion: tides are the product of  the gravitational interactions between the Earth and the Moon, with consequent emission of an undulatory perturbation. We shall not forget moreover that tidal effects lead to a transfer of rotational energy which in this case has slowed down the Moon’s rotation until it became synchronous to its revolution period.

In the PSR 1913+16 system, both the reduction of the orbital period and the induced space-time distortion can also be considered to be tidal effects. Until the system’s influence on the motions of nearby bodies is not ascertained, we will not be able to exactly understand the ways energy is transferred, also because when a body exerts a gravitational influence on the motion of other objects it will receive an influence of the same global intensity.

A more daring extension of this hypothesis, but one substantially in line with relativity’s essential definition of gravitation as the curvature of space-time, and not as a force, states that no energy release through gravitational waves occurs; if energy loss is detected within the system, this should be attributed in a more traditional fashion to the emission of electromagnetic radiation or jets of matter. So, let’s see how the observed effects may be explained.

An accelerated mass will determine a deformation in the curvature of the space in which nearby objects move, thus modifying their orbits. These will in turn modify the curvature of the space in which the accelerated mass moves, fitting its orbit to the new geometrical configuration; in the case of PSR 1913+16 by reducing the orbital period. The orbital period’s reduction corresponds to the decrease of the orbit’s medium radius and the increase in rotational speed, but the angular momentum remains constant, with no gravitational energy transfer. Being  and  the orbit’s initial values and  and  the successive values, we obtain the angular momentum per mass unit  l  :

An extremely relevant consequence rules out that the modifications of the space curvature induced by an accelerated mass on surrounding bodies and the adaptation of the curvature near the mass may occur in succession at finite speeds, imposing their synchrony. A delay between the produced modification and the return reaction would cause a gravitational and energetic unbalance  with catastrophic consequences.

But even if they do not transmit energy directly, gravitational waves change the paths of objects, particles, and energy exchanges, so that the apparent  effect is analogous. In other words, an object can be moved by applying a force onto it, or by re-shaping the path along which it is moving, obviously causing it to shift direction or to change speed.

If some form of energy is needed to operate such changes in space geometry, this energy is yet to be discovered, and we currently have no clue as to what it is like.

In any case, the search for relativistic gravitational waves looks like a nearly desperate enterprise, not just because of the extreme faintness of their signal, but mainly because of their overlapping with the background noise (space is permeated by waves of the same type coming from every object in the universe) which makes it hard to detect such signals. And even after a signal is picked up, it will be extremely difficult to determine where it comes from and to associate it to an astronomical system or event. Some indications may be obtained by comparing the signals of different detectors, or from the characteristics of frequency, polarization, and intensity of waves emitted by systems whose structural features are already known.

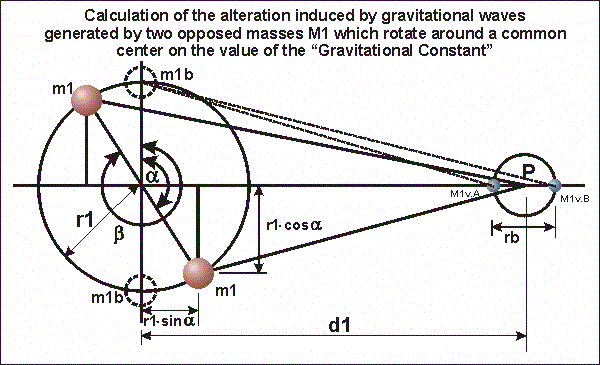
To better comprehend the action orbiting masses exert on surrounding objects, and to assess their actual entity, I have carried out some quantitative tests on a hypothetic pair of neutron stars, similar to the PSR 1913+16 pair but belonging to a theoretical system in which masses, orbits, and the features of the two stars are not altered by different origins or by correlated astronomical events.

The system would exhibit the following characteristics:

·        Mass of each of the two stars m1 = 1.4 M$ (solar masses) equal to  kg.

·        Radius r1 (distance from the center of mass) of the perfectly circular orbit 1,000,000 km.

·        Distance d1 from Earth 250 light years equal to km.

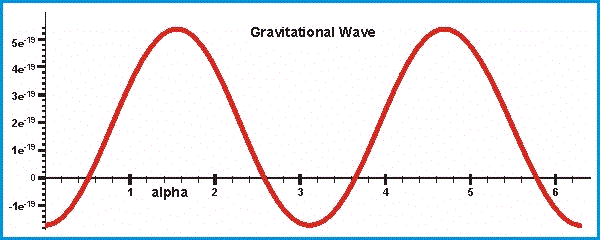
Figure AA

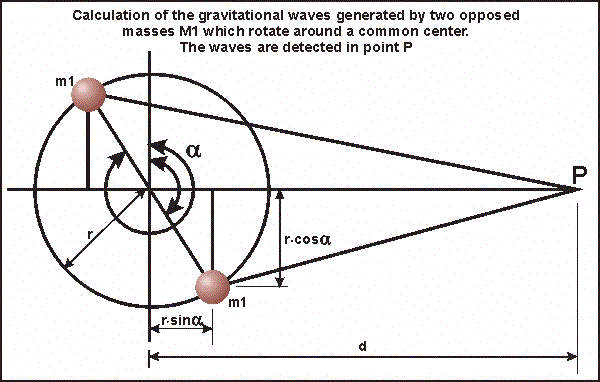
The calculation verifies the oscillations of an equivalent virtual mass , (by equivalent virtual mass we mean the mass that a hypothetical body would have if placed in the spot where the gravitational effect is measured which would produce the same effect of one or more distant bodies).

 measured in point P has the value:

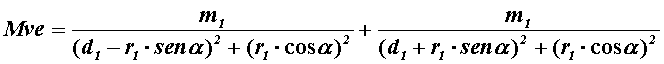
and for a complete rotation of the system, the equivalent virtual mass will exhibit the oscillation shown in the curve below. Masses are expressed in kg and distances in km; the oscillation is considered with respect to the continuous base value given by:

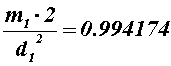
Two very important considerations stem from these simple calculations, the first of which concerns the influences of field oscillations on the value of the gravitational constant. In fact, if we determine the value of the virtual mass in points M1v.A and M1v.B, which represent two bodies placed at a mutual distance of 10 m and centered on point P (see figure BB below), we will observe an oscillation of the virtual mass’s value of  kg, still with respect to the base value of  kg.

The virtual mass will alter the mass of an object moving with respect to the two surrounding objects with an effective mass constituted by the sum of the two masses, the real and the virtual one. The gravitational constant G, derived from the force of attraction F measured between two bodies of masses m₁ and m₂ placed at a distance of:

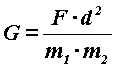
thus becomes a variable independent of the oscillations induced on masses m₁ and m_2.

Under normal conditions and at normal distances the values at play are so small that they are irrelevant, and any effect they may cause can only occur within time frames as long as the predicted age of the universe, or even longer. But in galactic nuclei, like in any other setting with an extremely high massive concentration, or in extrapolations on cosmological scales, the role of the variable G may become so relevant that any assessment error can be misleading.

Figure BB  

Another equally relevant consideration concerns the origin of relativistic gravitational waves, i.e. of the metric oscillations of the structure of space-time produced by the motions of accelerated masses.

In this case, deriving d from the equation for the determination of G and multiplying it by the ratio between gravitational force and electromagnetic force, we will obtain , i.e. the metric variation of space-time produced by the tidal effect on the distance d.

This way, the perturbation of the gravitational field not only affects the bodies’ mutual positions, but also acts on the very structure of matter.

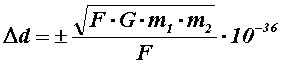
The search for relativistic gravitational waves with big interferometers however should not lead us to underestimate laboratory experiments, which can be carried out at a lower cost and with fewer resources. Clearly, in a laboratory it is not possible to detect relativistic waves, i.e. the metric distortion of the space-time, which can only be derived theoretically from the determination of the equivalent virtual mass.

The hypothetical system for laboratory trials is structured as in Figure AA, with two masses m1_a of 2000 kg each, radius r1_a of 10 meters, distance d1_a of 100 meters.

The equivalent virtual mass measured in P_a exhibits a continuous base value of 0.4 kg whereas the wave has a peak value of 0.0162 kg.

Laboratory trials would also allow to test other gravitational characteristics, such as the patterns in which the space curvature produced by a mass will follow this mass as it moves through space. To my knowledge, such a test has never been carried out so far. Let us discuss what should be verified, and why this research is so essential.

Gravitation is not determined by classic forces, but by space geometry which configures the bodies’ orbits. In detail, in a system like the one portrayed in figure CC 1 the star S will curve the space within which planets A and B move, thus re-shaping their orbits; the planets in turn influence space, thus perturbing the star’s orbit.

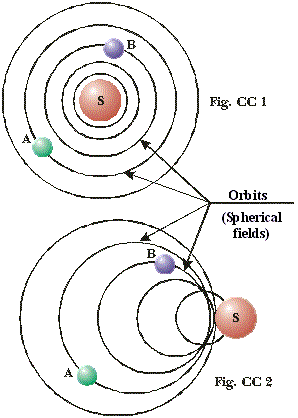
The star S however is itself moving along a galactic orbit, or along an orbit of the higher system that comprises it. The Sun, for instance, moves along the galactic orbit at about 230 km/s, our galaxy is moving at a speed of approximately 600 km/s in the Local Group, while the Local Group is in turn approaching the “Great Attractor” at an estimated  speed of about 2000 km/s. All these speeds, with respect to any external system of reference, may add or subtract according to the orbital position.

In order for planets A and B to maintain their orbits around the star S, the curvature of space imprinted by the star must follow it synchronously. If the curvature, or more precisely the gravitational field, was influenced at a finite speed, the two planets A and B would end up orbiting in a decentralized space because of the delay with respect to the star, entering a spiral orbit which would eventually cause them either to fall onto the star or to be expelled from the system, as shown in figure CC.

 Laboratory experiments - for which the proposed system is only one of the settings we could use to evaluate obtainable results – if properly designed and done with the most up-to-date equipment, should allow the relatively easy verification of gravitational interactions which govern the structure of our universe.

(To INDEX)